Displaying items by tag: return
Wednesday, 05 July 2017 05:00
Should I pay my student loans first or invest in the market?
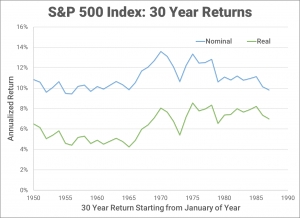
This is a common question that I get from my colleagues. To answer this question, I use a statistical approach to provide a conservative estimate of the threshold at which you would define as your "high-interest debt." If a loan has an interest rate higher than this, then you pay it down first. If the interest rate is lower, then you invest in the markets first.
Published in
Investing